My Five Achievements

A comprehensive library for reduced order modeling in Julia

I am the author of GridapROM.jl, a Julia-based library for the numerical approximation of parameterized partial differential equations using a broad range of reduced order modeling techniques. The library is designed to be both extensible and user-friendly, featuring a high-level, expressive API that promotes rapid prototyping without sacrificing performance. Thanks to Julia's just-in-time (JIT) compilation and advanced lazy evaluation strategies, GridapROMs delivers high efficiency while remaining fully written in Julia. The framework is PDE-agnostic and supports a wide spectrum of applications, including linear and nonlinear problems, single- and multi-field systems, and both steady-state and time-dependent formulations.

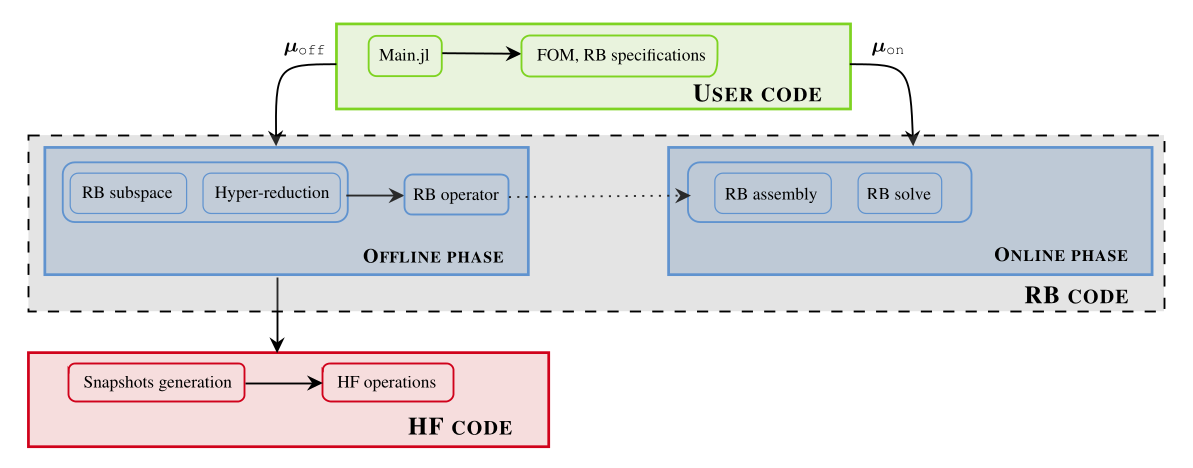Figure 1: A schematic view of the implementation of GridapROMs.

One of the key innovations of the library lies in the efficient generation of high-fidelity snapshots for parameterized partial differential equations. This is achieved through the lazy evaluation of cell-wise quantities defined over the finite element mesh, significantly reducing computational overhead during data assembly. In parallel, the integration of message-passing interfaces (MPI) enables scalable snapshot generation even for extremely large datasets – potentially comprising billions of entries in time-dependent problems – at fine spatial and temporal resolutions. As a result, the library effectively addresses one of the major computational bottlenecks in reduced order modeling: the cost of generating high-fidelity training data.

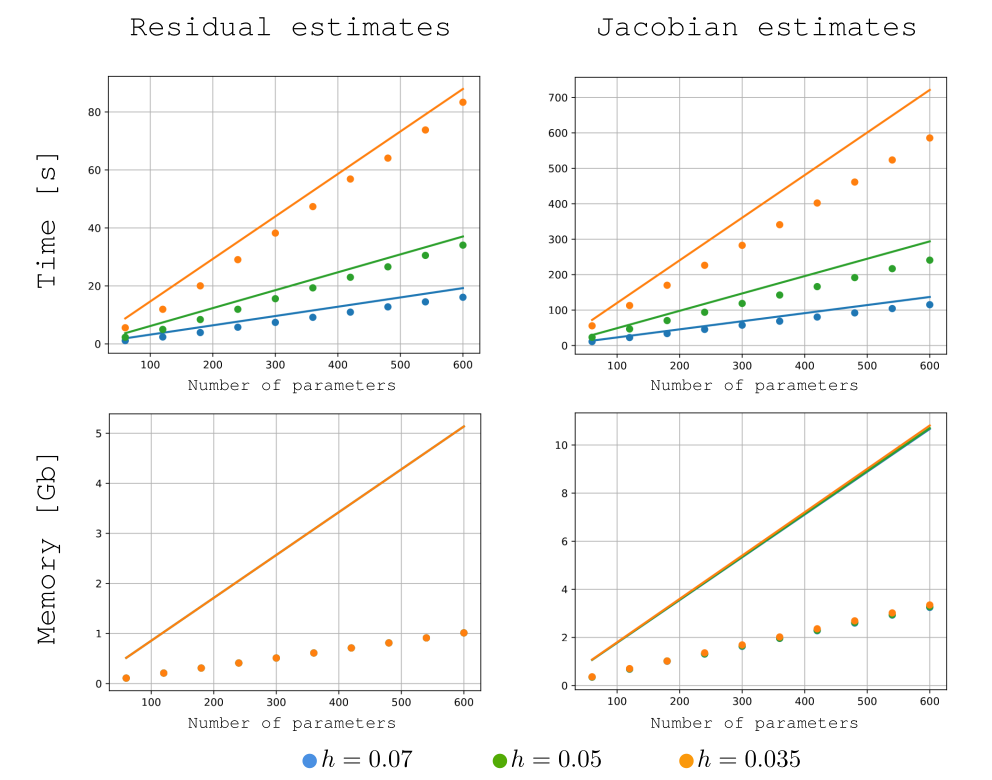Figure 2: Wall time and memory usage for residual and Jacobian assembly in GridapROMs.jl evaluated on a steady, parameterized Navier–Stokes problem in a 3D geometry, across different mesh resolutions. These measurements are benchmarked against a baseline estimate (solid lines), defined as the cost of assembling a single residual or Jacobian, scaled by the number of parameter instances. The results demonstrate that GridapROMs.jl significantly reduces both wall time and, even more notably, memory usage – highlighting the library's efficiency in handling large-scale parameterized problems.

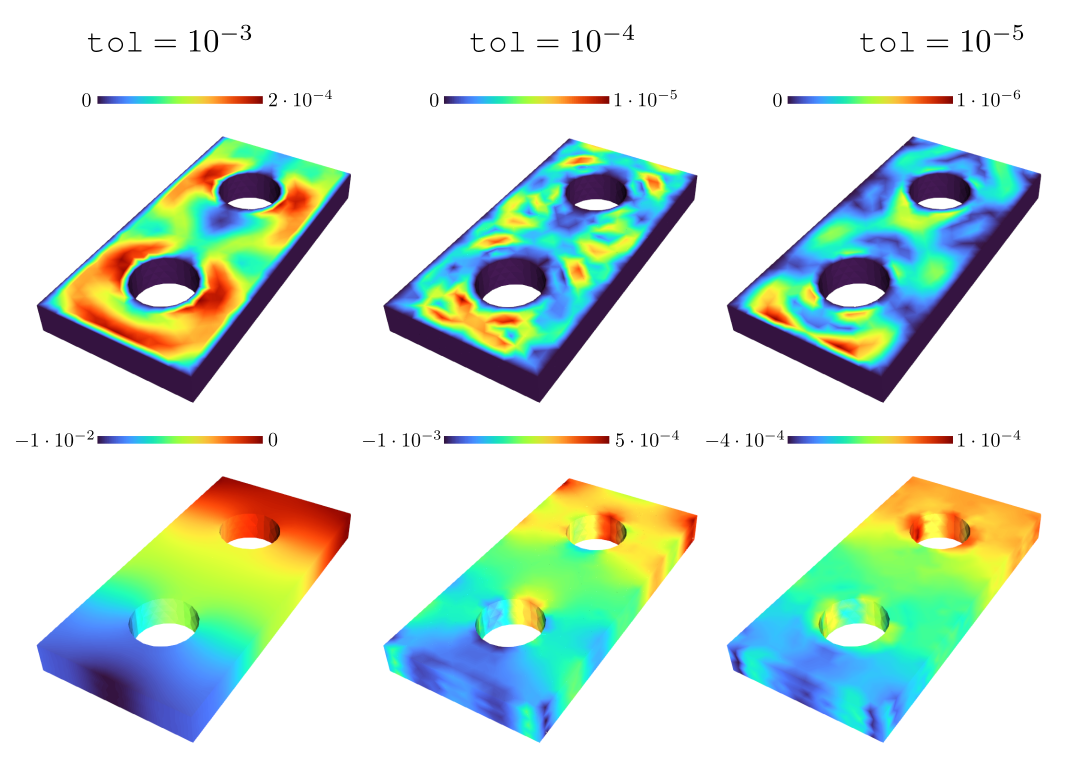Figure 3: Pointwise error between the finite element solution and the corresponding reduced-order approximations computed with GridapROMs.jl, for a fixed parameter and time instance in an unsteady, parameterized Navier–Stokes problem. The top row displays the velocity magnitude error for varying accuracy tolerances $\varepsilon = \{10^{-i}\}_{i=3}^{5}$, while the bottom row shows the corresponding pressure field error. These results illustrate the effect of the tolerance parameter on the accuracy of the reduced-order solution.

Cutting-edge advancements in reduced basis methods for problems defined on parameterized domains

Parameterized domains make solving partial differential equations (PDEs) especially challenging: geometric variations complicate traditional reduced-order models, remeshing is often required for each new configuration, and advanced tensor-based methods struggle on non-Cartesian grids. To tackle these issues, I designed a unified framework that combines unfitted finite element methods – where geometries are embedded in a background Cartesian mesh – with deformation-based mappings that transport a reference configuration to any parametrized domain. This innovation ensures that all solution data remain in a fixed-dimensional space, enabling the effective use of both classical and tensor-based reduced basis techniques.

I further enhanced the framework with a localization strategy that builds dictionaries of reduced subspaces and compressed operators, significantly boosting both accuracy and efficiency. I extended the methodology to complex saddle-point problems, including the Stokes and Navier-Stokes equations, through a tailored stabilization procedure. Extensive numerical experiments on benchmark fluid dynamics problems confirm that the approach delivers high accuracy and dramatic computational savings, even for complex parametrized geometries.

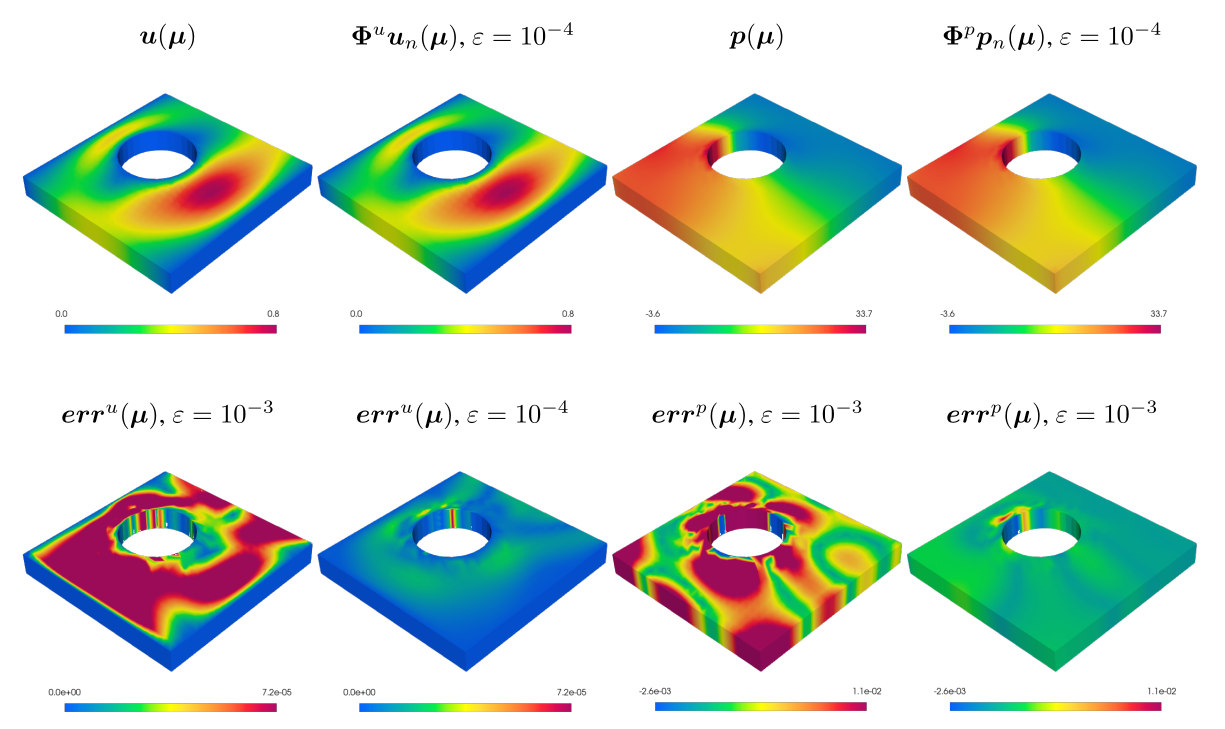Figure 4: Results for the Stokes equation, on a 3D rectangular geometry with a moving cylindrical hole. Top row: finite element velocity magnitude (left), reduced basis velocity magnitude (centre-left), finite element pressure (centre-right), and reduced basis pressure (right); the reduced basis velocity and pressure are obtained with an error tolerance $\varepsilon = 10^{-4}$. Bottom row: point-wise velocity error magnitude (left, with a tolerance $\varepsilon = 10^{-3}$, and centre-left, with a tolerance $\varepsilon = 10^{-4}$), and point-wise pressure error (centre-right, with a tolerance $\varepsilon = 10^{-3}$, and right, with a tolerance $\varepsilon = 10^{-4}$). Value of the test parameter: $\bm{\mu} = (0.63, 0.81)^T$.

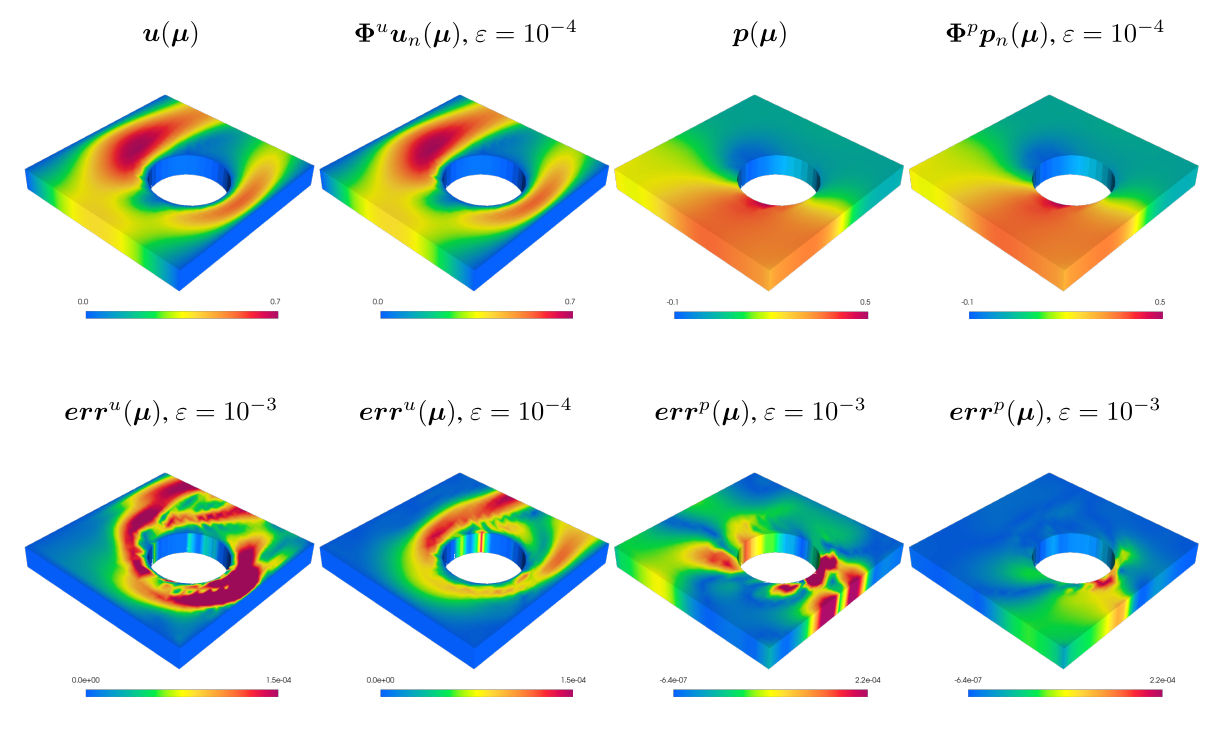Figure 5: Results for the Navier-Stokes equation benchmark, on a 3D rectangular geometry with a moving cylindrical hole. Top row: finite element velocity magnitude (left), reduced basis velocity magnitude (centre-left), finite element pressure (centre-right), and reduced basis pressure (right); the reduced basis velocity and pressure are obtained with an error tolerance $\varepsilon = 10^{-4}$. Bottom row: point-wise velocity error magnitude (left, with a tolerance $\varepsilon = 10^{-3}$, and centre-left, with a tolerance $\varepsilon = 10^{-4}$), and point-wise pressure error (centre-right, with a tolerance $\varepsilon = 10^{-3}$, and right, with a tolerance $\varepsilon = 10^{-4}$). Value of the test parameter: $\bm{\mu} = (0.62, 0.73)^T$.

The successful integration of tensor-train decompositions with reduced basis methods

I developed a novel reduced basis solver for efficiently solving parameterized partial differential equations by leveraging the tensor-train format to compactly represent high-dimensional finite element data. This approach yields several key benefits: a substantially more efficient construction of reduced subspaces, a cost-effective hyper-reduction technique for assembling full-order residuals and Jacobians, and a lower-dimensional projection space for a given target accuracy. The method is robust and exhibits convergence rates comparable to those of classical reduced basis methods. It has recently been integrated into GridapROM.jl.

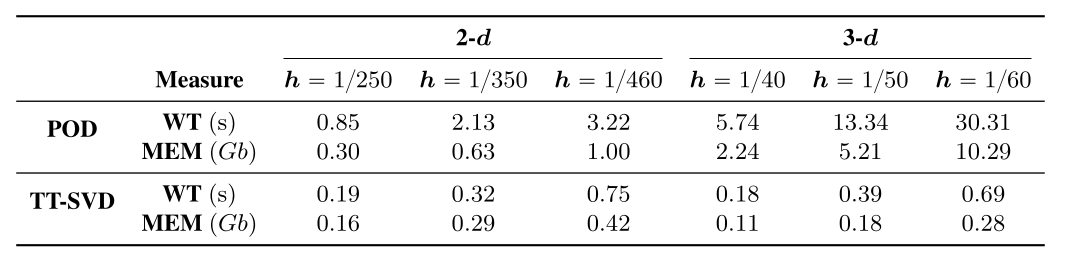Figure 6: From top to bottom: wall time (WT) and memory allocations (MEM) for constructing an $H^1$-orthogonal basis using both truncated POD and the tensor-train SVD, applied to a Poisson equation. From left to right: results are shown for 2D and 3D geometries across varying mesh sizes $h$, with a fixed accuracy tolerance of $\varepsilon = 10^{-4}$. The results highlight the superior computational efficiency of the tensor-train approach in both runtime and memory usage, compared to the traditional POD-based method.

Cutting-edge advancements in reduced order models for space-time problems

I contributed to the development of advanced reduced order models for the solution of parameterized, unsteady partial differential equations. The main contributions include:

• The proposal of a novel discrete interpolation method for the joint space-time approximation of finite element residuals and Jacobians.

• The development of stabilized reduced basis methods for the efficient solution of hemodynamics problems in arterial blocks. These methods significantly enhance the efficiency of traditional spatial-only reduced basis schemes, while maintaining comparable accuracy.

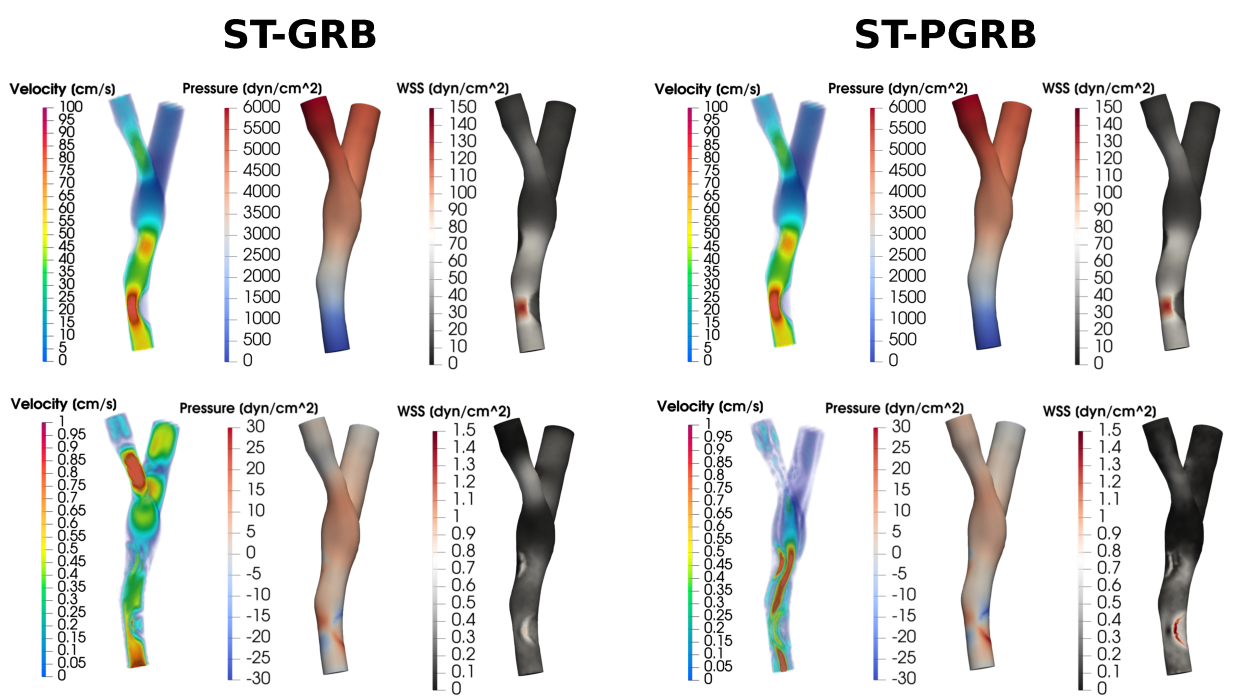Figure 7: Pointwise error between the finite element solution at a fixed parameter and time for an unsteady, parameterized Stokes equation solved in a Femoropopliteal Bypass, and the corresponding reduced-order solutions computed using a space-time Galerkin reduced basis method (left) and a space-time Petrov-Galerkin reduced basis method (right), across various accuracy tolerances. The first row reports the velocity magnitude errors for tolerances $\varepsilon = \{10^{-i}\}_{i=3}^{5}$, while the second row displays the corresponding pressure field errors.

A topology optimization library for generating compliant mechanisms in Matlab

As part of a 6-month internship at CSEM, I developed a topology optimization code in Matlab for designing novel compliant mechanisms tailored to aerospace applications. The generated designs were required to simultaneously satisfy multiple compliance constraints and pass manufacturing-level stress tests, which were carried out using Comsol Multiphysics.

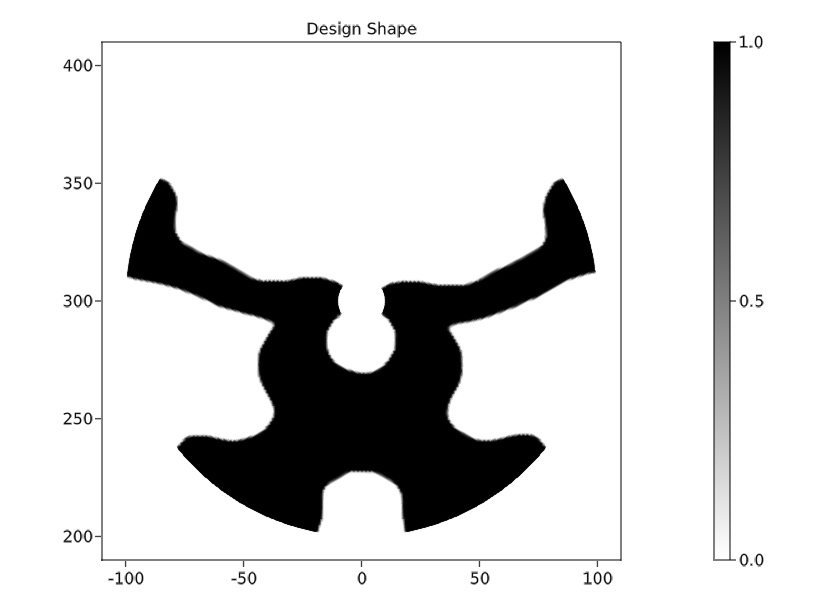Figure 8: A compliant mechanism generated with topology optimization.